10000

Ok hotshot, this is it, the only thing standing between you and slightly less internet anonymity.

We are provided with an exe that's slightly over 1GB. Despite this, IDA's autoanalysis completes rather quickly, and the main function is unobfuscated.

This makes IDA MCPs ideal for analyzing and renaming functions!

The program reads a file license.bin that must be exactly 340,000 bytes, then computes its SHA256 hash:

cinit(argc, argv, envp);
LODWORD(v3) = cout_write_string(Format_0, "checking license file...");
(cout_flush_endl)(v3);
mode = sub_1400C7D60(4u, 2);
ifstream_open(stream, "license.bin", mode);
stream_get_size(size_info, stream);
size = get_file_size(size_info);
if ( size == 340000 )
{
  sub_14007ECE0(stream, 0, 0);
  buffer = operator_new(size);
  stream_read(stream, buffer, size);
  sha256(buffer, buffer + 340000, hash_out, stream, 0x100000);
  buffer_1 = buffer;
  v23 = number_struct;

This license.bin should contain 10000 entries of the following form:

struct input_line
{
  __int16 index;
  char input[32];
};

The entries are then processed in a loop:

bignum_init(&bignum, 10000, number_struct);
for ( iteration_index = 0; iteration_index <= 9999; ++iteration_index )
{
    index = buffer_1->index;
    if ( index > 9999u )
      goto die;
    get_mask(&number_struct[1], &bignum, index);
    if ( mask_intersects_flags(&number_struct[1]) )
      goto die;
    get_mask(&outMask, &bignum, index);
    apply_mask(&outMask, 1);
    buffer_1 = (buffer_1 + 2);
    v24 = dynamic_pe_loader_and_iat_resolver(index);
}

Here, the first check enforces that all 10,000 entries have unique indices using bitmasks.

Next, the dynamic_pe_loader_and_iat_resolver function is called to retrieve a DLL based on the provided index.

This function takes in a resource ID (resId), which is the index from license.bin entries. It first checks an in-memory registry to determine if it had loaded this resource ID before. If this check is successful, the cached DLL is returned:

// dynamic_pe_loader_and_iat_resolver
end_it = ctx_get_value_from_field8((__int64)&registry_);
begin_it = ctx_get_value(&registry_);
it1 = loader_registry_find_by_id(begin_it, end_it, resId);
it2 = ctx_get_value_from_field8((__int64)&registry_);
if ( !ctx_values_equal((__int64)&it1, (__int64)&it2) )
    return *(_OWORD **)ctx_value_get_ptr(&it1);

If the resource is not found in the cache, it is loaded from the binary's resources and decompressed:

hResInfo = FindResourceA(0, (LPCSTR)resId, (LPCSTR)0xA);
hResData = LoadResource(0, hResInfo);
*(_QWORD *)&in_size[1] = LockResource(hResData);
in_size[0] = SizeofResource(0, hResInfo);
size = lz77_parse_compressed_data(*(const unsigned __int8 **)&in_size[1], in_size[0], 0);
init_output_buffer(&opts, size);
in_base = (unsigned __int8 *)alloc_uncompressed_buffer(&opts, 0);
lz77_decompress_to_buffer(*(const unsigned __int8 **)&in_size[1], (unsigned __int64)in_base, in_size[0], size, 0);

The resultant DLL is then loaded into memory using typical dynamic PE loading techniques. However, the import loading process is worth going over:

if ( (unsigned int)(*String - 48) > 9
    || (unsigned int)(String[1] - 48) > 9
    || (unsigned int)(String[2] - 48) > 9
    || (unsigned int)(String[3] - 48) > 9 )
{
    hModule = LoadLibraryA(String);
    while ( *v49 )
    {
    v19 = &out[(_QWORD)*v49];
    ProcAddress = GetProcAddress(hModule, v19 + 2);
    *v49++ = ProcAddress;
    }
}
else
{
    n0x270F_2 = atoi(String);
    v23 = dynamic_pe_loader_and_iat_resolver(n0x270F_2);
    while ( *v49 )
    {
    v22 = &out[(_QWORD)*v49];
    ctx = (__int64)(v23 + 1);
    x_1 = x;
    string_from_checked_input(x_2, v22 + 2, x);
    v21 = *(INT_PTR (__stdcall **)())get_function_from_dll(ctx, (__int64)x_2);
    string_destroy((__int64)x_2);
    *v49++ = v21;
    }
}

If the import name starts with 4 decimal digits, the typical LoadLibraryA process is skipped. Instead, dynamic_pe_loader_and_iat_resolver is called recursively to load the DLL from 10000.exe's resources. This explains the binary's large size: it contains 10,000 embedded DLLs (0000.dll through 9999.dll)!

This process can repeat multiple times, as the imported DLL can import more DLLs and so on.

Once the DLL and its imports have been completely resolved and mapped into memory, the DllMain function is invoked with import_counter as input. The DLL is then added into the registry to be cached.

v31 = &out[*((unsigned int *)image_base + 10)];
v30 = ((__int64 (__fastcall *)(_DWORD *, __int64, _QWORD))v31)(import_counter, 1, 0);
loader_registry_push_back_or_grow((__int64)&registry_, (__int64)&element_handle);

Back in main, the check function of the DLL corresponding to the input index is invoked. It must return 1 for validation to succeed.

ctx = (v24 + 1);
*&x[1] = x;
string_from_checked_input(&outMask.modulus_ptr, "_Z5checkPh", x);
checker = get_function_from_dll(ctx, &outMask.modulus_ptr);
LODWORD(ctx) = (*checker)(buffer_1) ^ 1;
string_destroy(&outMask.modulus_ptr);
if ( ctx )
    goto die;
buffer_1 = (buffer_1 + 32);
update_import_counter(iteration_index);

The update_import_counter function is called with the number of entries that have already passed validation (iteration_index).

void update_import_counter(int iteration_index)
{
  __int64 it2; // [rsp+20h] [rbp-20h] BYREF
  __int64 it1; // [rsp+28h] [rbp-18h] BYREF
  unsigned __int16 *v3; // [rsp+30h] [rbp-10h]
  __int64 registry; // [rsp+38h] [rbp-8h]

  registry = (__int64)&registry_;
  it1 = ctx_get_value(&registry_);
  it2 = ctx_get_value_from_field8((__int64)&registry_);
  while ( !ctx_values_equal((__int64)&it1, (__int64)&it2) )
  {
    v3 = *(unsigned __int16 **)ctx_value_get_ptr(&it1);
    import_counter[*v3] += iteration_index;
    VirtualFree(*((LPVOID *)v3 + 1), 0, 0x8000u);
    sub_140020560(&it1);
  }
  sub_1400AF7B0(&registry_);
}

For each imported DLL in the registry, the import_counter array at the corresponding index is incremented by iteration_index. The registry is then cleared so the next entry is processed with a fresh DLL import cache.

This is crucial, after processing all 10,000 entries, the import_counter must match a hardcoded expected value.

if ( memcmp(import_counter, &expected, 40000u) )
{
die:
    LODWORD(v9) = cout_write_string(Format_0, "invalid license file");
    ((void (__fastcall *)(__int64))cout_flush_endl)(v9);
    v6 = 1;
    goto LABEL_13;
}

This means the entries in license.bin must be ordered correctly to must pass all 10,000 DLL check functions and produce the correct import_counter values.

A Graph Problem

Before we even begin to deal with any graphs, we need to extract and decompress the DLLs from the binary. I used GitHub Copilot with the IDA Pro MCP to analyze and implement the decompression process in Python. While it took a few tries to get it right due to the nonstandard compression algorithm, it was eventually able to extract and decompress all 10,000 DLLs.

Next, I used pefile to parse each DLL's imports and exports, writing the results to JSON. Multiprocessing accelerated this step.

You can find the code implementing this here

We now have a JSON file containing a list of imports for each of the DLLs. Our import graph problem can now be modelled using the following code:

# graph is a directed acyclic graph in adjacency list form, where the keys of the dictionary are the node IDs, and the values are the connected nodes.
# The graph and expected array are fixed and cannot be changed.

assert len(set(inputs)) == 10000
assert len(inputs) == 10000

import_counts = [0 for _ in range(10000)]
for i in range(10000):
    handled = set()
    def handle(idx):
        if idx in handled:
            return
        handled.add(idx)
        import_counts[idx] += i
        for dep in graph.get(idx, []):
            handle(dep)
    handle(inputs[i])

assert import_counts == expected

I used an LLM to generate a solver that performs topological sorting to find the correct entry order. After ~10 minutes, it produced a valid solution!

DLL Analysis

Loading up 0000.dll in IDA and decompiling the check function, we first observe a sequence of about 600 function calls acting on the input string (a1):

While most of the functions can be found within 0000.dll, some of them are imported from the other embedded DLLs.

Fortunately for us, each function falls into one of three categories:

• Substitution: Each byte is replaced via a lookup table
• Permutation: Bytes are rearranged to different positions
• Modular exponentiation: The 32-byte input is treated as a 256-bit little-endian number and raised to power $e$ modulo $2^{256}$

All three operations are easily reversible.

Here is an example from f63971385288077461058, which performs modular exponentiation:

There are two important details:

1. The first DWORD is XORed with a value pointed to by qword_224186020, which holds the import_counter from DllMain. Different DLLs add an offset to reference their specific import count. We must track this to recover the XOR key.
2. The exponent loads in 8-byte chunks. However, the 3rd and 4th stores write at offsets 15 and 23 respectively, causing an overlap. This means the exponent is actually only 31 bytes long.

Manually extracting constants from 10,000 DLLs with hundreds of functions each is infeasible. Instead, I exploited the fact that functions within the same category are nearly identical, differing only in constants.

I sampled 3 functions from each category, identified byte offsets where all differed, then applied these offsets to other functions in that category to extract their constants. Byte-matching also identifies which category each function belongs to.

This approach requires no disassembly or decompilation, enabling rapid extraction across all DLLs.

The end result was 10,000 JSON files, each containing constants extracted from the corresponding DLL. Here's an excerpt from 0.json:

{
  "_Z21f00158157358463794801Ph": [
    "sbox",
    "1cbbc15d938a0ccfa0660661462ed765f7f974a93310816c4b3f16bf7849d5f8aa3153e71291ec5fd39d1f8ee6201bb557e856ab6b805445733a4aca3b5ad919dded509535b970c9ce3899266f6823f60d3d51c489442d84c29863c5ea32ac522a3621b6b2fa60186e9c7511349be9f17130b708e242f51d77be7daec68fcd769e64cbf347af4d6a58fe075e1a29e4a78cdc038b14b4a1b8558309a4d0922b7a37b3f4d4de87d6fc48ba4f7cbca6e15bccd262d8c3df220af0001e2f2c28b0417ec07b13ef4e9a05023e79da43fbe58869156782c7240e860494ee39a57feb5c0fa29f9617f29027db8559e36da33ce0a8b10b01ffadd14cbdfd258dc8974072"
  ],
  "_Z21f00468644590832420931Ph": [
    "permute",
    "030c0814151f13160f041800091d1b0717191c051a01060e120a10111e0d020b"
  ],
  "_Z21f00593041430746087033Ph": [
    "sbox",
    "1327a82ff2720df0b5a3d9d025bc674ac4eb3cbf00ee1a2ca909fc79da3171d35e405691489b10c8bae8938ee5a2c98316ce88fa34bbd89db31d8d51d2ccf71b9ae63d0142b25a61298530332a7398eadfa68fc547be5f2d4f657ea5143a23190b411e6af18203db875411554cca0e46abddd5d1f9b16d5396fbdc7a4443056e95685c4ef37db9772b3ffeed805949d412a4849c261797ad6f74f56b90fd8b20e769c7814de335159fdec158aa5d8acf6c383be0ef7fffa73921d65be4664b072eb87c7b0af4b0b645f662cd18c2e908c0c3d704941f927689326360a0ecae8602e1ac522250bde28c28c6579e06751c703799b4b764a1af360f24f8783e0ccb"
  ],
  "_Z21f00665857230930416977Ph": [
    "modexp",
    26878308109340952526170247771787660207614205310038810462299392579812584108215
  ],
  "_Z21f00747197010245102126Ph": [
    "modexp",
    14414409544188964954310982741996758062091641366334423162439729811158806413771
  ],
  "_Z21f00792437605780649147Ph": [
    "permute",
    "1d100e1a071218041e0016110a0f05191f0b030c080206010d1c13171415091b"
  ],

What functions are called?

The next step is to determine which transformation function is called at each step. We need a fast approach for all 10,000 DLLs.

Assembly call patterns follow two forms:

1. Direct call:

   .text:000000022417ACD0                 mov     rcx, rax
   .text:000000022417ACD3                 call    _Z21f62734954317222471872Ph

   By matching the mov rcx, rax; call pattern, we can determine the function's address.

2. Call to imported function

   .text:000000022417ACBD                 mov     rcx, rax
   .text:000000022417ACC0                 mov     rax, cs:_Z21f35937321701949324150Ph 
   .text:000000022417ACC7                 call    rax

   Matching the mov rax, cs:...; call rax pattern identifies the imported function.

A Matrix Problem

After the ~600 transformation rounds, the input is XORed against a hardcoded constant array:

The array contains 16 QWORDs (128 bytes), but the input is only 32 bytes. The XOR key repeats every 4 QWORDs, suggesting a 4×4 matrix structure.

A long and complicated sequence of calls follow. Using the IDA MCP to analyze this reveals that it implements modular exponentiation on a 4x4 matrix.

Hidden within the function are a few clues that confirm this hypothesis:

1. A value computed from the matrix is compared against 0. If it equals 0, the check function returns. This matches the check for an invertible matrix, which fails if the determinant of the matrix is 0.
2. The result array is initialized to the identity matrix.
3. Back in the xor loop, the function returns if any element within the matrix exceeds the modulus (a 16 byte integer stored in v255). The other integer, v254, is the exponent.

Finally, the result matrix is compared against a target matrix:

At this point, the elements of the matrices have been upgraded to 16-byte wide integers, though the upper 8 bytes are all zero as the modulus is less than $2^{64}$.

As before, byte-matching quickly extracts matrix constants across all DLLs.

However, reversing matrix modular exponentiation differs from scalar exponentiation. Normally, we compute:

$$\begin{array}{rl}c& =m^e\mathrm{mod}p\\ d& =e^{-1}\mathrm{mod}(p-1)\\ m& =c^d\mathrm{mod}p\end{array}$$

Unfortunately, this formula does not work for matrix modular exponentiation. In this case, we are working in the General Linear Group. The order of the group would be the number of 4x4 invertible matrices. Since invertible matrices have to be linearly independent, the order can be computed as:

$$(p^4-1)(p^4-p)(p^4-p^2)(p^4-p^3)$$

Substituting this formula allows us to correctly compute the inverse exponent and reverse the matrix exponentiation.

Putting It Together

Working backwards from the recovered input matrix, we can reverse the XOR to find the state after transformation. Using the known import count, we then reverse all transformations to find the original input.

This script took ~30 minutes to generate license.bin. However, running 10000.exe directly would be too slow due to the DLL import process.

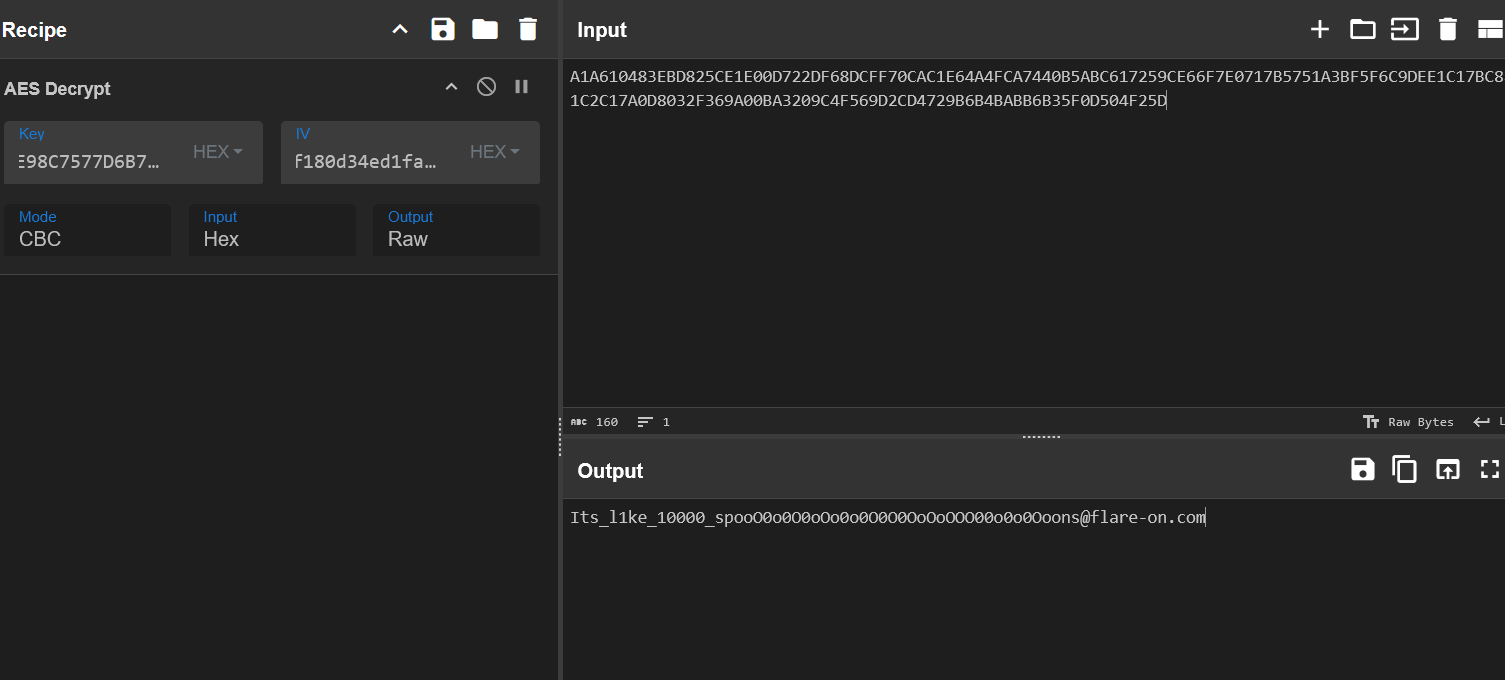
Instead, we can further analyze the main function to determine that the SHA256 hash of license.bin is used as the key for AES-256-CBC decryption with the following parameters:

CT = A1A610483EBD825CE1E00D722DF68DCFF70CAC1E64A4FCA7440B5ABC617259CE66F7E0717B5751A3BF5F6C9DEE1C17BC881C2C17A0D8032F369A00BA3209C4F569D2CD4729B6B4BABB6B35F0D504F25D
IV = 78615338bcb1f180d34ed1fa47a41d3d
KEY = SHA256(license.bin) = 600ABF28E03C73471A73BB909210DC2D2B4E98C7577D6B71299D2E54D693D14D

Plugging these values into CyberChef reveals the flag: